线性代数的本质4：点积与对偶性

向量的点积又称数量积、内积。点积有两种定义方式：代数方式和几何方式。
向量的点积既可以由向量坐标的代数运算得出，也可以引入向量的长度和夹角的几何概念来求解。
二维向量的点积 $a \cdot b = x_1x_2 + y_1y_2 = | a | | b |\cos{\theta}$
无论根据哪一种定义都容易证明点积运算满足交换律和分配律 (不满足结合律)。
下面证明两个定义的等价性。

从几何定义推导坐标公式

设$a = (x_1, y_1)$, $b = (x_2, y_2)$, $\hat{i}$, $\hat{j}$为单位基向量，
由点积的几何定义 $\hat{i} · \hat{i} = | \hat{i} || \hat{i} | \cos{0} = 1, \quad \hat{j} · \hat{j} = | \hat{j} | | \hat{j} | \cos{0} = 1$，
$\hat{i} · \hat{j} = | \hat{i} | | \hat{j} | \cos{\dfrac{\pi}{2}} = 0$，
由向量坐标的定义，$a = x_1\hat{i} + y_1\hat{j}, \quad b= x_2\hat{i} + y_2\hat{j}$ ,
$\because$ 点积满足分配率
$\begin{align} \therefore a \cdot b &= (x_1\hat{i}+y_1\hat{j})\cdot(x_2\hat{i}+y_2\hat{j}) \\ &=x_1x_2(\hat{i}\cdot\hat{i})+x_1y_2(\hat{i}\cdot\hat{j})+x_2y_1(\hat{i}\cdot\hat{j})+y_1y_2(\hat{j}\cdot\hat{j}) \\ &= x_1x_2 + y_1y_2 \end{align}$

从坐标定义推导几何公式 （推广到n维）

n维向量夹角的定义

设$a$和$b$为两个任意非零n维向量，以$a$，$b$，$a-b$ 三向量的模长为边可构成三角形。
(利用三角不等式$|x + y| \le |x| + |y|$证明任意两边之和大于等于第三边，即可证能构成三角形)
向量$a$和$b$的夹角定义为这个三角形中长为$|a|$和$|b|$的两邻边夹角$\theta$。
由余弦定理，$|a-b|^2 = |a|^2 + |b|^2 - 2|a||b|\cos{\theta}$
由点积的坐标定义，
$\begin{align}|a - b|^2 &= (a - b) \cdot (a - b) \\ &= a \cdot a - a \cdot b - b \cdot a + (-b) \cdot (-b) \quad (点积满足乘法分配律)\\ &= |a|^2 - 2(a \cdot b) + |b|^2 \qquad (1) \\ &= |a|^2 + |b|^2 - 2|a||b|\cos{\theta} \qquad (2) \end{align}$
等式$(1)(2)$两边消去得：$a \cdot b = |a|\,|b|\cos{\theta}$

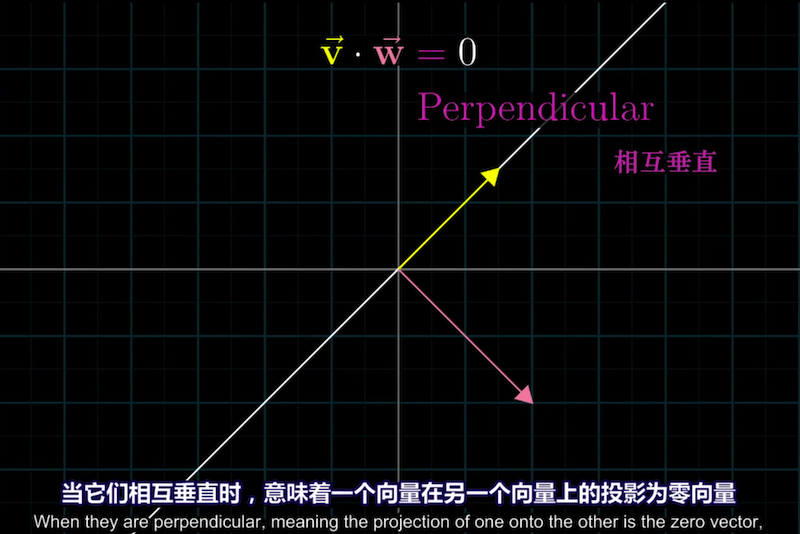
补充1：n维向量正交的概念

基于n维向量夹角的定义，定义n维向量垂直的概念：
若两非零向量$a$和$b$夹角为90度则称$a$和$b$互相垂直。
由点积的几何公式有$a \cdot b = 0$ 即 两向量垂直 $\iff$ 两向量点积为0
零向量与任何向量正交。

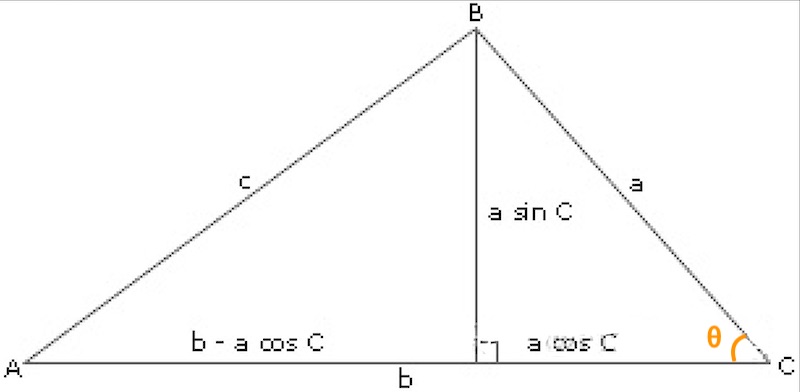
补充2：余弦定理的证明

如图，由勾股定理：
$\begin{align} c^2 &= (a\sin{\theta})^2 + (b-a\cos{\theta})^2 \\ &= a^2\sin^2\theta + b^2 - 2ab\cos\theta + a^2\cos^2\theta \\ &= a^2(\sin^2\theta + \cos^2\theta) + b^2 - 2ab\cos\theta \\ &=a^2 + b^2 - 2ab\cos\theta \end{align}$

补充3: Cauchy-Schwarz不等式

不等式$|x \cdot y | \le |x|\,|y|$ 对$\forall$ 非零向量$x,y \in \mathbb{R}$都成立，
当且仅当$x = cy$时，即$x,y$共线时等号成立。
证明： 根据点积的性质 (向量自身的点积等于模长的平方），
注意到$\forall \,t \in \mathbb{R}$ 都有 $(x+ty)\cdot(x+ty) = |x+ty|^2 \ge 0$
$(x+ty)\cdot(x+ty)=x\cdot x+x\cdot ty+ty\cdot x +ty \cdot ty$
$= |x|^2 + 2t(x\cdot y) + t^2|y|^2 \ge 0$
以$t$为自变量变形为二次不等式：$p(t) = |y|^2t^2 +2(x\cdot y)t + |x|^2 \ge 0$
令$a = |y|^2,\,b = 2(x \cdot y),c=|x|^2$
$\because y$是非零向量 $\therefore a = |y|^2 > 0$ $p(t)$开口向上
$\because p(t) \ge 0$ $\therefore$ 一元二次方程根的判别式$\,\Delta = b^2-4ac \le 0$
代入得：$[2(x \cdot y)]^2 -4|y|^2|x|^2 \le 0$
$4(x \cdot y)^2 - 4|x|^2|y|^2 \le 0$ 即 $|x \cdot y| \le |x|\,|y|$ 恒成立。
(根据点积的几何定义也可证明)

补充4：三角不等式

三角不等式： $|\vec{v}+\vec{w}| \le |\vec{v}|+|\vec{w}|$ 等号成立当且仅当其中一向量 为另一向量的非负倍数。 $\begin{align} \textbf{证明：}|\vec{v}+\vec{w}|^2 &= (\vec{v}+\vec{w})\cdot(\vec{v}+\vec{w})=|\vec{v}|^2+2\underline{\vec{v}\cdot\vec{w}}+|\vec{w}|^2 \hspace{50em} \\ &\le |\vec{v}|^2+|\vec{w}|^2+2|\vec{v}\cdot\vec{w}| \\ &\le |\vec{v}|^2+|\vec{w}|^2+2|\vec{v}||\vec{w}| \quad (\text{Cachy-Schwarz}不等式)\\ &=(|\vec{v}|+|\vec{w}|)^2 \end{align}$ $\therefore |\vec{v}+\vec{w}| \le |\vec{v}|+|\vec{w}|$ 等号成立当且仅当$\vec{v}\cdot\vec{w}=|\vec{v}||\vec{w}|$,
这等价于$\vec{v},\vec{w}$其中一向量是另一向量的非负倍数。

注：基于Cauchy-Schwarz不等式可证明三角不等式，基于三角不等式
可定义n维向量夹角，从而推出向量点积的几何公式。

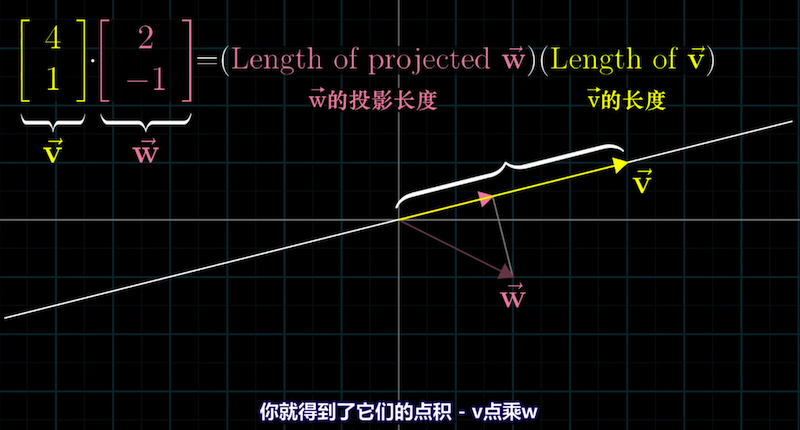
向量点积的几何直观

向量长度和另一向量投影长度之积

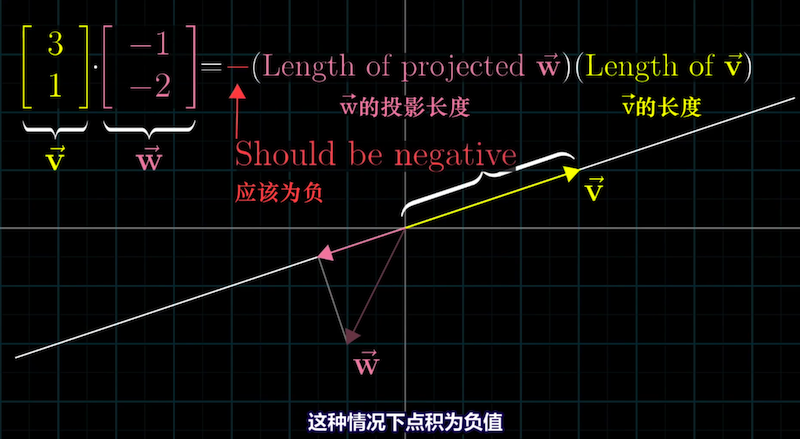
投影方向与被投影向量相反时，即两向量夹角大于90度时，点积为负值

当两向量互相垂直时，投影为零向量，点积为0

用投影解释向量点积的几何公式显得很”不对称”，因为$a$投影到$b$还是$b$投影到$a$都不影响计算结果。
为什么点积的结果与投影的方式无关呢？
先来看两向量等长的情况，沿着夹角平分线作对称轴，分别画出两向量之间的投影，
根据三角形全等的条件(两角一边)，发现两种投影方式互为镜像，这种情况显然不影响结果。

现在把其中一个向量缩放若干倍。如下图，把短的向量投影到长的向量上，
此时$(k\vec{v})\cdot \vec{w} = k(\vec{v} \cdot \vec{w})$，因为缩放一个向量k倍并不会改变另一个向量的投影长度,
相当于把原来对称情况下的点积乘以k倍。

反过来把长向量投影到短向量上，根据相似三角形，$\vec{v}$ 在 $\vec{w}$上的投影被放大了2倍，
对短向量长度仍不变，相比镜像对称的情况，效果仍然是把原来的点积放大了2倍。
因此，无论哪种投影方式，缩放向量（破坏对称）对点积结果的影响都一样，
也就是说即使向量不等长，投影方式不同也不影响点积的结果。

直观理解坐标公式与几何投影的联系

假设我们不知道点积的几何定义，仅知道点积的坐标公式。
为什么将对应坐标相乘再将结果相加的计算过程，与投影有联系？
最令人满意的答案来自对偶性(duality)。
这种点积与投影（线性变换）的关系在于将其中一向量倾倒，
就得到对另一向量作投影变换的$1 \times n$矩阵。

首先来看多维空间到一维空间（数轴）的线性变换。
不少函数都能接收2维向量并输出一个数，但线性变换的要求更加严格，
需满足性质$L(\vec{v}+\vec{w}) = L(\vec{v})+L(\vec{w})$和$L(c\vec{v}) = cL(\vec{v})$
本篇仅考虑与之等价的直观特性，即“保持原点不变且网格线平行等距分布”，二维到一维的
变换情况就是任意二维向量所在直线上等距分布的点，经过线性变换后也等距分布于数轴上。
变换后的基向量落在数轴上变成一个数，用一个$1 \times 2$矩阵描述。

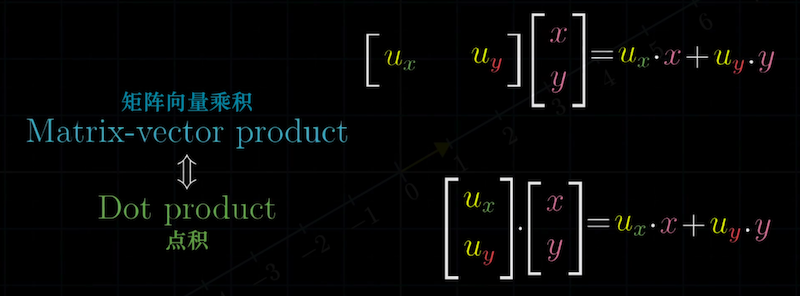
$\mathbb{R}^2 \rightarrow \mathbb{R}$的线性变换用$1 \times 2$矩阵与向量的乘法描述，其运算方法(列的线性组合)
看起来就和点积的坐标公式一样。$1 \times 2$矩阵看起来正像一个倾倒的向量。

通过以上观察发现，点积的坐标公式与$\mathbb{R}^2 \rightarrow \mathbb{R}$变换的$1 \times 2$矩阵向量乘法运算具有相同的形式。
下面我们从几何直观上验证一下2D投影矩阵左乘2D向量其实就是2D投影矩阵的行向量与
这个向量的对应坐标相乘再相加，从而确定点积的几何解释就是投影长度与向量模长之积。

假定你还不知道点积与投影有关，考虑0在原点斜放的数轴上一个单位向量(模长为1的向量）$\hat{u}$

如果我们把二维向量投影到这条数轴上，就定义了一个从二维向量到数字的变换，
通过视觉上的检验，发现这个投影变换是线性的。（直线上等距分布的点投影到数轴上仍保持等距）
注意u帽是输入空间中一个二维向量，只是刚好让它落在输出空间数轴上。
下面我们来找出这个投影变换对应的投影矩阵。

考虑变换后单位基向量$i$帽和$j$帽的位置，它们将分别变成矩阵的两列（两个数）。

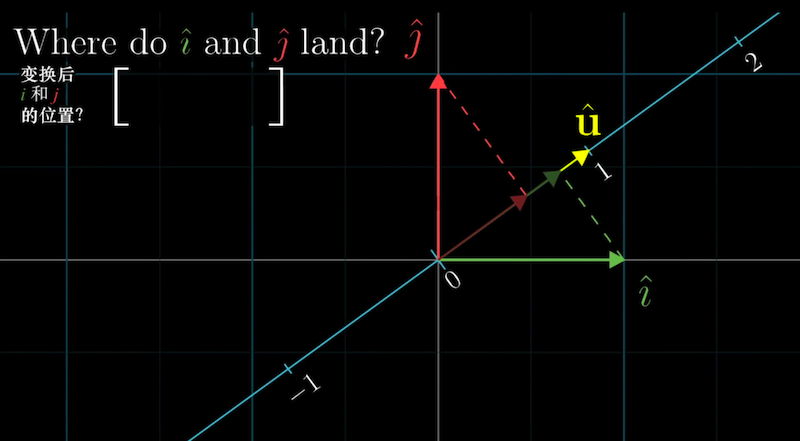
因为$\hat{i}$ 和 $\hat{u}$都是单位向量，它们之间的互相投影存在之前提到过的镜像对称关系，
$\hat{i}$在$\hat{u}$上的投影长度其实就是$\hat{u}$的横坐标$u_x$，同理，$\hat{j}$ 在$\hat{u}$上的投影长度等于$\hat{u}$的纵坐标$u_y$

因此投影变换矩阵就是$\bigl[\begin{matrix} u_x & u_y \end{matrix}\bigr]$，所以任意二维向量与单位向量的点积，
都可解释为将向量投影到单位向量所在直线上所得到的投影长度（可正可负）

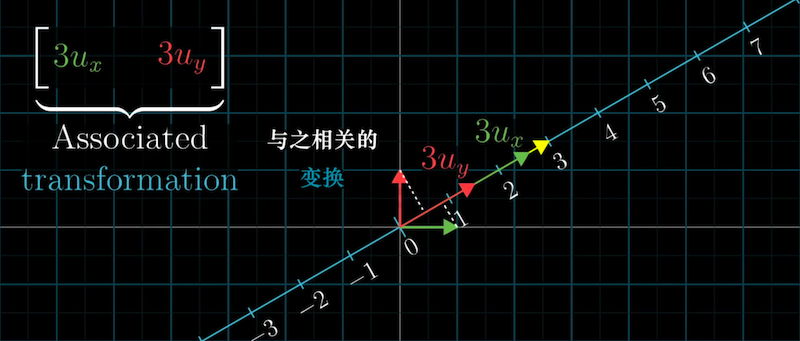
如果是与“非单位向量”的点积，对偶的变换是$\bigl[\begin{matrix} ku_x & ku_y \end{matrix}\bigr]$，即基向量的投影长度分别是$u_x$和$u_y$的$k$倍。

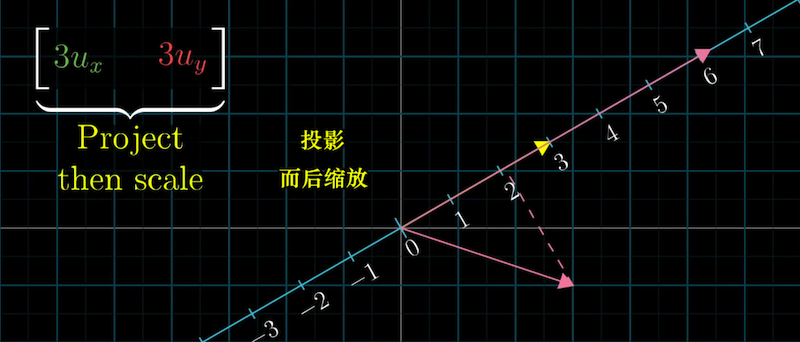
因为变换是线性的，即$\bigl[\begin{matrix} ku_x & ku_y \end{matrix}\bigr] = k\bigl[\begin{matrix} u_x & u_y \end{matrix}\bigr]$, 这个变换等价于先将二维向量投影到单位向量，
再把投影长度乘上k倍。单位向量的缩放倍数k即“非单位向量”的模长，所以任意两个向量点积的
几何解释就是投影长度与向量长度的乘积，从而得到点积的几何公式$|a||b|\cos{\theta}$

对点积的直观几何解释用到了对偶性的思想。
对偶性是两个数学事物之间存在的自然而又出乎意料的对应关系。
两个向量的点积，利用向量与线性变换的对偶关系，相当于把其中一个向量看作是投影变换矩阵。
于是，我们可以进一步地理解向量的本质是“线性变换的物质载体”。
（as the physical embodiment of a linear transformation”）
向量就像一个特定变换的概念性记号，例如本节中转置成$1 \times 2$矩阵的二维向量就是投影变换的记号。
一个2d-to-1d的线性变换，必存在一个唯一的向量，
输入向量与这个对偶向量点积与应用变换的效果是一样的。

duality 这个概念在数学和物理的许多地方都有分布，而没有一个统一的定义。我熟悉的 duality 大部分都是
把两个显然相对应的东西联系起来，有时这两个东西在某种程度上甚至是等价的（比如在同构意义上）。
因为一旦有了对偶性，每证明一个定理都能通过对偶的操作自动免费得到另一个（可以理解为镜像）。
数学的布尔代数和集合论中的对偶概念可能是最平易近人的。
物理中常翻译为二象性，例如波粒二象性 (Wave–particle duality)。